PyTorch at Gideon in 2021: A year in review

Get an insight into what happened in the PyTorch community throughout 2021 from the perspective of the Gideon AI team.

Written by

Valentina Zadrija, Ph.D.

Senior Machine Learning Engineer

January, 28th, 2022

After almost a decade of research in deep learning, Tensorflow and PyTorch have emerged as the two most prominent frameworks for training deep learning models.

We at Gideon use both interchangeably for prototyping and production – gotta use the best tool for the task.

This blog post represents a year’s review of what happened in the PyTorch community throughout the last year from the perspective of the Gideon AI team.

Due to its simplicity and eager execution, the PyTorch is extremely popular, both by researchers and deep learning practitioners. In the last year, we have witnessed three major releases from PyTorch 1.8 in March to PyTorch 1.10 in October each of them comprising over 3000 commits. So what’s new? Stay tuned and keep on reading.

What’s new in PyTorch?

PyTorch offers a plethora of features for training deep neural networks – loss functions, normalizations, metrics; you name it.

In 2021, we observed a slight shift from a pure deep learning paradigm towards scientific computing, linear algebra, signal processing, and complex numbers.

Since we at Gideon are developing deep learning models for 3D scene understanding, we have found many of these new features super useful, especially torch.linalg and torch.fft.

But let us first start with a pure deep learning feature – deferred initialization.

Deferred initialization in PyTorch

Deferred initialization has been available for a long time in deep learning frameworks like Tensorflow, Keras, or MXNet. There you could blissfully define your model and let the framework infer the input dimensions at runtime.

PyTorch did not support this functionality prior to 1.8 version, when they introduced the torch.nn.Lazy* modules. Truth be told, these modules are still under heavy development, but nevertheless, now you can use the LazyConv2d instead of your favorite Conv2d without the need to specify the number of input channels.

Let us see some examples of how this works. Say that we have some input embeddings of different sizes (e.g. in_size ∈ [64, 128, 300, 600]) as shown in the code snippet below:

                    
import torch
 
# input features in batches of 3
batch_size = 3
input_embeddings = [
    torch.randn(batch_size, 64),  # in_size = 64
    torch.randn(batch_size, 128), # in_size = 128
    torch.randn(batch_size, 300), # in_size = 300
    torch.randn(batch_size, 600), # in_size = 600
]

Next, for the sake of the example, we define a simple network without specifying the input feature dimensions in_size. So instead of using torch.nn.Linear(in_size, 128) in the first network layer, we simply omit the number of input features and use torch.nn.LazyLinear(128).

                    
def net():
    dense_model = torch.nn.Sequential(
        torch.nn.LazyLinear(128),
        torch.nn.ReLU(),
        torch.nn.LazyLinear(32),
        torch.nn.ReLU(),
        torch.nn.LazyLinear(30),
        torch.nn.ReLU(),
    )
    return dense_model
 
dense_net = net()

The PyTorch will defer the initialization (each parameter od the dense_net will be an instance of torch.nn.parameter.UninitializedParameter), waiting for the first time we pass the input embeddings through the network. Then it will infer the weight sizes of each layer on the fly. As the code snippet below shows, we can then use the same network definition net() regardless of the input size:

                    
for embedding in input_embeddings:
    dense_net = net()
    out = dense_net(embedding)
    weights_shape = dense_net[0].weight.shape
    print(f"Input size: {embedding.shape[0]} x {embedding.shape[1]},",
          f"Weights size: {weights_shape[0]} x {weights_shape[1]}")

Hence, the above code generates neural networks of different weight shapes for the same network definition, leading to the following output:

                    
Input size: 3 x 64,  Weights size: 128 x 64
Input size: 3 x 128, Weights size: 128 x 128
Input size: 3 x 300, Weights size: 128 x 300
Input size: 3 x 600, Weights size: 128 x 600

This allows us to potentially skip some boilerplate code and focus on the core functionality that we want to implement.

Right, let’s dig into the hard-core computer vision problems, feature extraction for general visual representations.

Looking for a general visual representations? Extract features without tampering the code

What makes a cat, a person, a forklift, a trailer, a building, or a road an object? When you look at this question, it may seem like we are trying to solve an eternal philosophical dilemma of the universe :).

Alas, we are looking for a general visual representation of such objects. This is often the first step in various computer vision tasks: from object detection, semantic and instance segmentation to 3D reconstruction and pose estimation.

To capture these general features, we usually start with a so-called backbone network that can be trained on a large dataset for some generic task like image classification. This is a simple task, which allows us to infer something like this: “There is a person somewhere in the image”.

Sometimes we may want to detect smaller and, at different times, larger objects. To do that, we want to extract these generic visual representations called features at various levels of complexity. This is where feature extraction comes into the game.

There are different ways how to extract intermediate features from the network in PyTorch, to name a few:

• use the source Luke way, i.e., perform the model surgery by modifying the source code for the network (i.e., forward methods of modules),
• attach forward hooks to modules, or
• use torchvision.models.feature_extraction module.

Modifying the source code may be just fine when we know which features we exactly want to extract (in the final product). But, if you want to do quick prototyping, this will become cumbersome and ugly fast.

The hooks also bear their own set of problems (e.g., see the docs), but in essence, you still need to run the whole network to extract some intermediate feature. So here, we will focus on torchvision.models.feature_extraction module, which was introduced in PyTorch 1.10.

To extract features from a neural network, we first need to decide which model to use for the general visual representation, so let’s start with that. In 2021, there has been a lot of talk in the community about whether we can still use good old-fashioned convolutional architectures [1], [2] and obtain as good results as with the attention-based methods like transformers [3], [4] on small to medium datasets.

Wightman et al. [5] have shown that ResNets have indeed been mistreated as a baseline in many papers and proposed a bag of tricks to improve the ResNet training. Hence, we will use their ResNet-18 trained with an A1 bag of tricks. If you are interested in learning more details, please refer to the paper [5].

So let’s get coding: first, we start by creating a ResNet-18 model.

                    
import torch 
import timm 
from torchvision.models import resnet18 
from torchvision.models import feature_extraction as FE 
  
# instantiate a ResNet-18 
model = resnet18(pretrained=False) 
  
# load weights from Wightman et al. 
src = 'https://github.com/rwightman/pytorch-image-models'
model_pth = 'resnet18_a1_0-d63eafa0.pth'
checkpoint = f'{src}/releases/download/v0.1-rsb-weights/{model_pth}'
model.load_state_dict(torch.hub.load_state_dict_from_url( 
    checkpoint, progress=False)) 
model.eval()

We then use the get_graph_node_names function to construct a symbolic graph from the network by using the Torch FX toolkit under the hood. The Torch FX is a core PyTorch library that, in this case, applies the symbolic tracing of the ResNet Python code.

It analyzes operations (not just torch.nn modules but any operation like reshape or add), their dependencies, and constructs a graph from them.

Each operation in a graph is assigned a human-readable name which is then returned as a list element inside train_nodes and eval_nodes.

train_nodes, eval_nodes = FE.get_graph_node_names(model)

By inspecting the content of the train_nodes or eval_nodes, we can see that we obtain the names for each operation inside each layer, not just layer outputs. For example, results of the batch normalization layer1.0.bn2 or results of the skip connection layer1.1.add are intermediate ops inside the first layer.

So let’s extract some features (that’s what we’re here for). We do that by invoking the create_feature_extractor function:

                    
# choose some ops from the eval_nodes above 
node_names = ['layer1.1.add', 'layer2.1.conv1', 
              'layer3.0.downsample.0', 'layer4.1.conv1'] 
intermediate_nodes = FE.create_feature_extractor( 
    model, return_nodes=node_names)

This creates a new model intermediate_nodes and prunes all the operations from the original ResNet, which are not necessary for computing the outputs from nodes specified in the node_names list.

All the operations after the first convolution in the fourth layer are removed in this example. This is only logical – say we only want to extract features from the second layer, we do not need to evaluate all the layers afterward. We can then evaluate such a model on a couple of images and visualize the activations as shown below.

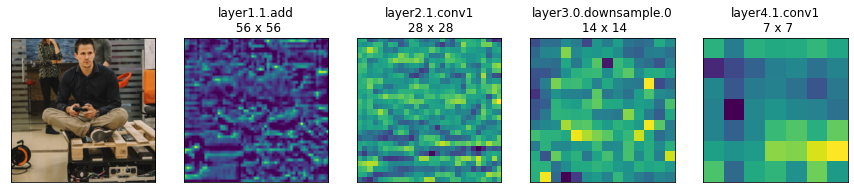
Examples of feature maps extracted at different stages of the network

The torchvision.models.feature_extraction based feature extraction is applicable to all models for which we can construct a static symbolic graph (for exceptions, we may bundle problematic ops into a leaf_node or wrap functions, see the docs). Similar workflow can also be applied for the transformer based architecture, for instance DeiT [4].

                    
# DeiT: Data-Efficient Image Transformer 
model_vit = timm.create_model( 
    'deit_small_patch16_224', pretrained=False) 
  
# load weights from Wightman et al. 
src = 'https://github.com/rwightman/pytorch-image-models'
model_pth = 'deit_small_patch16_a1_0-bfd3c1ab.pth'
checkpoint = f'{src}/releases/download/v0.1-rsb-weights/{model_pth}'
model_vit.load_state_dict( 
    torch.hub.load_state_dict_from_url(checkpoint, progress=False)) 
model_vit.eval() 
  
# extract features with torchvision.models.feature_extraction 
node_names_vit = ['patch_embed.norm', 'blocks.0.attn.qkv', 
                  'blocks.0.mlp.fc1',  'blocks.4.attn.proj',  
                  'blocks.11.mlp.fc2'] 
intermediate_blocks_vit = FE.create_feature_extractor( 
    model_vit, return_nodes=node_names_vit)

Now that we got that out of the way let’s dig into scientific computing topics – starting with linear algebra.

Bye bye `numpy.linalg`, hello `torch.linalg`

The torch.linalg is the PyTorch linear algebra module which became stable in PyTorch 1.9. It contains a superset of linear algebra operations supported in numpl.linalg. Remember numpy.linalg.solve? PyTorch now supports full-fledged differentiable GPU and CPU implementations. To check how fast it actually is, we have tested its performance against NumPy counterparts on a laptop machine with an Intel i7-10750H CPU @ 2.60GHz and NVIDIA GeForce GTX 1660 Ti GPU.

Let’s see it in action! Say we want to solve a system of n linear equations,

?⋅?=?

where ?∈ℝ^n×3×3 and ?∈ℝ^n×3×1 are known, and we want to solve for ?. In PyTorch, we can do that with the following code snippet:

                    
import torch 
  
# generate some data: n samples in the batch 
n = 10
A = torch.randn(n, 3, 3).cuda() 
b = torch.randn(n, 3, 1).cuda() 
  
# solve for x 
x = torch.linalg.solve(A, b) 
  
# verify 
torch.allclose(A @ x, b)

Now we compare the performance in terms of execution time with the well known numpy.linalg.solve on CPU. On the y axis we show the ratio between the execution times in numpy and torch implementations (higher ratio values indicate that the torch implementation is faster).

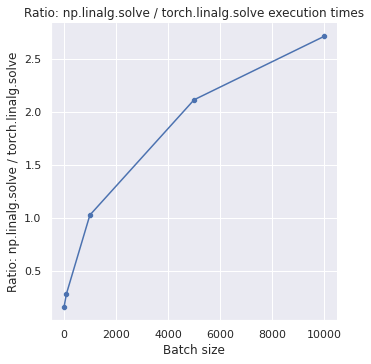
torch implementation graph gpu against cpu

Performance benchmarking of torch.linalg.solve on a GPU against numpy.linalg.solve on a CPU: higher y values indicate that the torch implementation is faster.

The results show that the torch implementation works faster for batches with more than 1000 samples; anything below it is even slower.

This is expected, as transferring the data to the GPU takes some time and is less efficient for smaller batches. So, should you use it or not, that depends on your use case. If you are performing triangulation of a large point cloud and want to compute the plane equations for each triangle, the PyTorch implementation may be a way to go.

Now, let’s check out what’s going on with signal processing support.

Signal processing with `torch.fft`, complex numbers

You probably remember the Fourier transform (FFT) from your signal processing graduate classes. Then you know it has numerous applications in audio, image processing, and physics. Since PyTorch 1.8, there’s a differentiable FFT implementation for both CPU and GPU.

So, you might ask yourself, what’s in it for me?

Well, one of the use cases where the FFT might really be useful is developing deep learning models for 3D pose estimation for autonomous mobile robots.

Let’s say you want to estimate the distance and rotation of an object (for example, a pallet, trolley, or a box) against the robot. If you choose to solve this problem with deep learning, one of the problems you may stumble upon is that widely used convolutional neural networks are not rotation equivariant. This means that if you rotate an image (or some other representation like a 3D point cloud), the corresponding CNN feature map will not rotate accordingly.

What can you do to tackle this problem? You can always collect more data, use data augmentations, or maybe you can change your data representation [6], [7], [8], [9], or even network representation [10].

If you choose the data representation path, you can project the data into a spherical domain, perform convolutions in a spectral domain by using the FFT and then obtain a representation that is sensitive to changes in rotation [6], [7] (the content of the cited papers is beyond the scope of this blog post, so we refer the interested reader to the papers).

A simple example of such a pipeline is shown in the image below, where we show rotation equivariant features for an airplane point cloud:

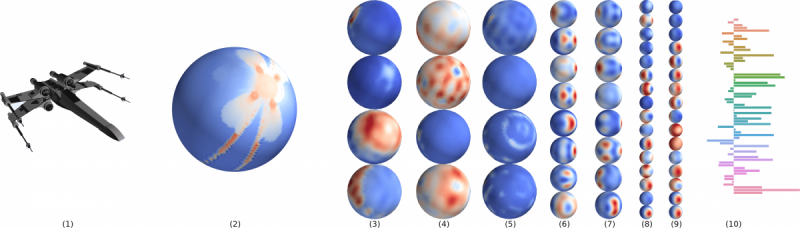
Learning SO(3) Equivariant Representations with Spherical CNNs: the 3D model (1) is mapped to a spherical function(2), which is then passed through a series of spherical convolutions generating rotation equivariant maps (3-9) suitable for rotation estimation. Image credit [7]

So far, the FFT has been implemented in SciPy, NumPy, JAX, and TensorFlow (most notably), so to make use of FFT, you had to use one of these frameworks. With the advent of PyTorch 1.8.0., the torch.fft module has become stable, allowing for PyTorch-based usages of the FFT.

We at Gideon believe that this is a part of a new trend in the PyTorch development: a shift from pure machine learning to signal processing and physics. Since PyTorch 1.9, support for complex numbers has also been added, and soon, discrete cosine transform (DCT) will also be supported. These are exciting news, so buckle up, Scotty!

How do we make our PyTorch code more efficient?

As shown throughout this blog post so far, Python and PyTorch as a framework built on top of it are great for trying out new deep learning models and methods.

There are a bunch of different libraries that allow you to do scientific computing, run computer vision algorithms, or solve ordinary differential equations, to name a few. But, to paraphrase Yann LeCun:

“To use Python as frontend for a numerical library is a terrible idea, it’s slow, it’s not compilable, and it’s not strongly typed, but Python is what people want.”

And this is what we at Gideon try to keep in mind when defining our deep learning models. We need to have the best of both worlds: the expressivity and extensibility of Python on one side and performance and efficiency on the other. So, let’s talk about the latter for a bit.

CUDA graphs: to execute eagerly, or not – that is the question

By far, one of the most popular PyTorch features is its eager execution. It allows us to debug the code easily and examine the variables’ content and shapes after executing each statement. This is great for debugging but comes at a cost (there’s no such thing as a free lunch): each eager op incurs a CPU overhead from Python to PyTorch backend and the CUDA driver.

So, what sometimes happens is that the GPU runs operations faster than the CPU can feed it, and utilization is poor – in other words, the performance is CPU-bound.

For network regions whose shapes and ops do not change across iterations, we don’t need to recompute the shapes and launch individual kernels every time, so most of the CPU work is redundant. This is where CUDA graphs come in: they allow us to record a dummy iteration of a training loop as a graph and replay it on the GPU. The CPU is free to do other tasks at this time: for instance, load a new batch of data from a DataLoader.

As Linus Torvalds once said, “Talk is cheap, show me the code”, so let’s dig into the code. Please note that the CUDAGraph PyTorch API is still in beta, and there may be changes in the future. Let us first create a dummy iteration with torch.empty placeholders and record it as a graph. The torch.cuda.graph context manager will do the actual recording.

                    
# create dummy data placeholders 
data_input = torch.empty(input_shape, device='cuda') 
data_label = torch.empty(output_shape, device='cuda') 
  
# dummy iteration 
g = torch.cuda.CUDAGraph() 
optimizer.zero_grad(set_to_none=True) 
with torch.cuda.graph(g): 
    y_pred = model(data_input) 
    loss = loss_fn(data_label, y_pred) 
    loss.backward() 
    optimizer.step()

Then we replay the graph on the actual data:

                    
for data, target in zip(real_inputs, real_targets):
    data_input.copy_(data)
    data_label.copy_(target)
    # replay the iteration
    g.replay()

Note that this implementation requires a warmup phase before the dummy iteration; please check the documentation for more details.

So great, CUDA graphs are awesome, right? There are the things to keep in mind however:

• the shapes must not change across iterations (otherwise, what’s the point),
• no dynamic control flow.

So what if we do have dynamic control flow statements in our train iteration? After all, those things are pretty standard in practice, right? In such cases, we can use torch.cuda.make_graphed_callables to convert partial code segments into CUDA graphs. The backward call is also executed as a graph. With torch.cuda.make_graphed_callables, there is no need for the warmup phase and explicit copying of the real data into placeholders as this is handled internally by the make_graphed_callables call.

So in a way, we achieve a semi-full circle: from eager execution mode to partial graph execution mode.

Conclusion

We did a quick recap of the new PyTorch features we used at Gideon last year. We are particularly excited about the new features added to torch.linalg and torch.fft modules. They will facilitate and speed up the development of deep learning models using the signal processing transformations like Fast Fourier transform and Discrete Cosine Transform (once the latter is fully supported).

We also believe that the feature extraction interface is an excellent addition as it works almost seamlessly with different kinds of architectures (both convolutional and transformer-based). This will definitely speed up the prototyping for various computer vision tasks.

Finally, two described features are still in diapers: the PyTorch support for CUDA graphs and the deferred initialization. The CUDA graphs feature could really help with the situations where the problem is CPU-bound and diminish the negative side effects of the eager execution.

On the other hand, deferred initialization is a nice-to-have feature because it allows an engineer to focus on solving the actual problem without the need to worry if the input feature dimensions have changed.

At the time of publishing this blog post, the PyTorch framework will probably turn 5 – and despite the ubiquitous problems that the Python language bears, it has been fun to use. We have also noticed that our skin is more radiant, our wrinkles have been reduced by 95%, our hair is shiny and full of life :).

WANT TO CREATE COOL ROBOTS? JOIN US

References

[1] K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” CoRR, vol. abs/1512.03385, 2015.

[2] A. Kolesnikov, L. Beyer, X. Zhai, J. Puigcerver, J. Yung, S. Gelly, and N. Houlsby, “Big transfer (BiT): General visual representation learning,” in Computer vision – ECCV 2020 – 16th european conference, glasgow, UK, august 23-28, 2020, proceedings, part V, 2020, vol. 12350, pp. 491–507.

[3] Z. Liu, Y. Lin, Y. Cao, H. Hu, Y. Wei, Z. Zhang, S. Lin, and B. Guo, “Swin transformer: Hierarchical vision transformer using shifted windows,” CoRR, vol. abs/2103.14030, 2021.

[4] H. Touvron, M. Cord, M. Douze, F. Massa, A. Sablayrolles, and H. Jégou, “Training data-efficient image transformers & distillation through attention,” in Proceedings of the 38th international conference on machine learning, ICML 2021, 18-24 july 2021, virtual event, 2021, vol. 139, pp. 10347–10357.

[5] R. Wightman, H. Touvron, and H. Jégou, “ResNet strikes back: An improved training procedure in timm,” CoRR, vol. abs/2110.00476, 2021.

[6] T. S. Cohen, M. Geiger, J. Köhler, and M. Welling, “Spherical CNNs,” in 6th international conference on learning representations, ICLR 2018, vancouver, BC, canada, april 30 – may 3, 2018, conference track proceedings, 2018.

[7] C. Esteves, C. Allen-Blanchette, A. Makadia, and K. Daniilidis, “Learning SO(3) equivariant representations with spherical CNNs,” in Computer vision – ECCV 2018 – 15th european conference, munich, germany, september 8-14, 2018, proceedings, part XIII, 2018, vol. 11217, pp. 54–70.

[8] M. Geiger, T. Smidt, A. M., B. K. Miller, W. Boomsma, B. Dice, K. Lapchevskyi, M. Weiler, M. Tyszkiewicz, S. Batzner, M. Uhrin, J. Frellsen, N. Jung, S. Sanborn, J. Rackers, and M. Bailey, Euclidean neural networks: e3nn. Zenodo, 2020.

[9] J. Lin, Z. Wei, Z. Li, S. Xu, K. Jia, and Y. Li, “DualPoseNet: Category-level 6D object pose and size estimation using dual pose network with refined learning of pose consistency,” CoRR, vol. abs/2103.06526, 2021.

[10] C. Deng, O. Litany, Y. Duan, A. Poulenard, A. Tagliasacchi, and L. J. Guibas, “Vector neurons: A general framework for SO(3)-equivariant networks,” CoRR, vol. abs/2104.12229, 2021.